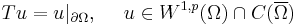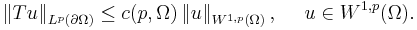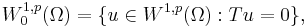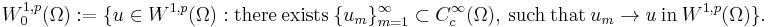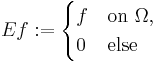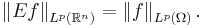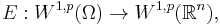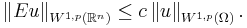Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space. Intuitively, a Sobolev space is a space of functions with sufficiently many derivatives for some application domain, such as partial differential equations, and equipped with a norm that measures both the size and regularity of a function.
Sobolev spaces are named after the Russian mathematician Sergei Sobolev. Their importance comes from the fact that solutions of partial differential equations are naturally found in Sobolev spaces, rather than in spaces of continuous functions and with the derivatives understood in the classical sense.
Contents |
Motivation
There are many criteria for smoothness of mathematical functions. The most basic criterion may be that of continuity. A stronger notion of smoothness is that of differentiability (because functions that are differentiable are also continuous) and a yet stronger notion of smoothness is that the derivative also be continuous (these functions are said to be of class C1 — see smooth function). Differentiable functions are important in many areas, and in particular for differential equations. On the other hand, quantities or properties of the underlying model of the differential equation are usually expressed in terms of integral norms, rather than the uniform norm. A typical example is measuring the energy of a temperature or velocity distribution by an L2-norm. It is therefore important to develop a tool for differentiating Lebesgue functions.
The integration by parts formula yields that for every u ∈ Ck(Ω), where k is a natural number and for all infinitely differentiable functions with compact support φ ∈ Cc∞(Ω),
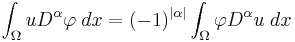 ,
,
where α a multi-index of order |α| = k and Ω is an open subset in ℝn. Here, the notation
is used.
The left-hand side of this equation still makes sense if we only assume u to be locally integrable. If there exists a locally integrable function v, such that
we call v the weak α-th partial derivative of u. If there exists a weak α-th partial derivative of u, then it is uniquely defined almost everywhere. On the other hand, if u ∈ Ck(Ω), then the classical and the weak derivative coincide. Thus, if v is a weak α-th partial derivative of u, we may denote it by Dαu := v.
The Sobolev spaces Wk,p(Ω) combine the concepts of weak differentiability and Lebesgue norms.
Sobolev spaces with integer k
Definition
The Sobolev space Wk,p(Ω) is defined to be the set of all functions u ∈ Lp(Ω) such that for every multi-index α with |α| ≤ k, the weak partial derivative 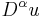 belongs to Lp(Ω), i.e.
belongs to Lp(Ω), i.e.
Here, Ω is an open set in ℝn and 1 ≤ p ≤ +∞. The natural number k is called the order of the Sobolev space Wk,p(Ω).
There are several choices for a norm for Wk,p(Ω). The following two are common and are equivalent in the sense of equivalence of norms:
and
With respect to either of these norms, Wk,p(Ω) is a Banach space. For finite p, Wk,p(Ω) is also a separable space. It is conventional to denote Wk,2(Ω) by Hk(Ω) for it is a Hilbert space with the norm 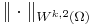 .[1]
.[1]
Approximation by smooth functions
A lot of properties of the Sobolev spaces cannot be seen directly from the definition. It is therefore interesting to investigate under which conditions a function u ∈ Wk,p(Ω) can be approximated by smooth functions. If p is finite and Ω is bounded with Lipschitz boundary, then for any u ∈ Wk,p(Ω) there exists an approximating sequence of functions um ∈ C∞(Ω), smooth up to the boundary such that ||um-u||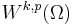 → 0.[2]
→ 0.[2]
Sobolev spaces with non-integer k
Bessel potential spaces
For a natural number k and 1 < p < ∞ one can show (by using Fourier multipliers[3][4]) that the space Wk,p(ℝn) can equivalently be defined as
with the norm
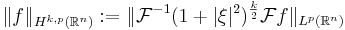 .
.
This motivates Sobolev spaces with non-integer order since in the above definition we can replace k by any real number s. The resulting spaces
are called Bessel potential spaces[5] (named after Friedrich Bessel) and are denoted by Hs,p(ℝn). They are Banach spaces in general and Hilbert spaces in the special case p = 2 .
For an open set Ω ⊆ ℝn, Hs,p(Ω) is the set of restrictions of functions from Hs,p(ℝn) to Ω equipped with the norm
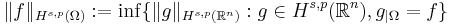 .
.
Again, Hs,p(Ω) is a Banach space and in the case p = 2 a Hilbert space.
Using extension theorems for Sobolev spaces, it can be shown that also Wk,p(Ω) = Hk,p(Ω) holds in the sense of equivalent norms, if Ω is domain with uniform Ck-boundary, k a natural number and 1 < p < ∞. By the embeddings
the Bessel potential spaces Hs,p(ℝn) form a continuous scale between the Sobolev spaces Wk,p(ℝn). From an abstract point of view, the Bessel potential spaces occur as complex interpolation spaces of Sobolev spaces, i.e. in the sense of equivalent norms it holds that
Sobolev–Slobodeckij spaces
Another approach to define fractional order Sobolev spaces arises from the idea to generalize the Hölder condition to the Lp-setting.[6] For an open subset Ω of ℝn, 1 ≤ p < ∞, θ ∈ (0,1) and f ∈ Lp(Ω), the Slobodeckij seminorm (roughly analogous to the Hölder seminorm) is defined by
![[f]_{\theta, p, \Omega}�:= \int_{\Omega} \int_{\Omega} \frac{|f(x)-f(y)|^p}{|x-y|^{\theta p %2B n}} \; dx \; dy](/2012-wikipedia_en_all_nopic_01_2012/I/3d44b259e7fed763320c81512de3349d.png) .
.
Let s > 0 be not an integer and set 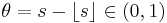 . Using the same idea as for the Hölder spaces, the Sobolev–Slobodeckij space[7] Ws, p(Ω) is defined as
. Using the same idea as for the Hölder spaces, the Sobolev–Slobodeckij space[7] Ws, p(Ω) is defined as
![W^{s,p}(\Omega)�:= \left\{f \in W^{\lfloor s \rfloor, p}(\Omega)�: \sup_{|\alpha| = \lfloor s \rfloor} [D^\alpha f]_{\theta, p, \Omega} < \infty \right\}](/2012-wikipedia_en_all_nopic_01_2012/I/ede5f5d695f11b9966b74c8b8c5b034c.png) .
.
It is a Banach space for the norm
![\|f \| _{W^{s, p}(\Omega)}�:= \|f\|_{W^{\lfloor s \rfloor,p}(\Omega)} %2B \sup_{|\alpha| = \lfloor s \rfloor} [D^\alpha f]_{\theta, p, \Omega}](/2012-wikipedia_en_all_nopic_01_2012/I/918ac8e7b13cdea61f8ff04615dd056e.png) .
.
If the open subset Ω is suitably regular in the sense that there exist certain extension operators, then also the Sobolev–Slobodeckij spaces form a scale of Banach spaces, i.e. one has the continuous injections or embeddings
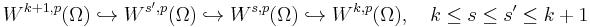 .
.
There are examples of irregular Ω such that 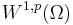 is not even a vector subspace of
is not even a vector subspace of 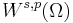 for
for 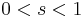 .
.
From an abstract point of view, the spaces Ws, p(Ω) coincide with the real interpolation spaces of Sobolev spaces, i.e. in the sense of equivalent norms the following holds:
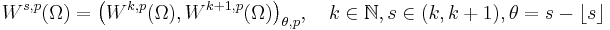 .
.
Sobolev–Slobodeckij spaces play an important role in the study of traces of Sobolev functions. They are special cases of Besov spaces.[4]
Traces
Sobolev spaces are often considered when investigating partial differential equations. It is essential to consider boundary values of Sobolev functions. If u ∈ C(Ω), those boundary values are described by the restriction 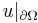 . However, it is not clear how to describe values at the boundary for u ∈ Wk,p(Ω), as the n-dimensional measure of the boundary is zero. The following theorem[2] resolves the problem:
. However, it is not clear how to describe values at the boundary for u ∈ Wk,p(Ω), as the n-dimensional measure of the boundary is zero. The following theorem[2] resolves the problem:
- Trace Theorem. Assume Ω is bounded with Lipschitz boundary. Then there exists a bounded linear operator
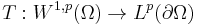 such that
such that
- and
Tu is called the trace of u. Roughly speaking, this theorem extends the restriction operator to the Sobolev space W1,p(Ω) for well-behaved Ω. Note that the trace operator T is in general not surjective, but maps for p ∈ (1,∞) onto the Sobolev-Slobodeckij space 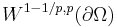 .
.
Intuitively, taking the trace costs 1/p of a derivative. The functions u in W1,p(Ω) with zero trace, i.e. Tu = 0, can be characterized by the equality
where
In other words, for Ω bounded with Lipschitz boundary, trace-zero functions in W1,p(Ω) can be approximated by smooth functions with compact support.
Extensions
For a function f ∈ Lp(Ω) on an open set Ω ∈ ℝn, its extension by zero
is an element of Lp(ℝn). Furthermore,
In the case of the Sobolev space W1,p(Ω), extending a function u by zero will not necessarily yield an element of W1,p(ℝn). But for Ω bounded with Lipschitz boundary, there exists for every 1 ≤ p ≤ ∞ a bounded extension operator[2]
such that
- Eu = u on Ω,
- Eu has compact support and
- there exists a constant c depending only on Ω and the dimension n, such that
Sobolev embeddings
It is a natural question to ask if a Sobolev function is continuous or even continuously differentiable. Roughly speaking, sufficiently many weak derivatives or large p result in a classical derivative. This idea is generalized and made precise in the Sobolev embedding theorem.
Notes
- ^ Evans 1998, Chapter 5.2
- ^ a b c Adams 1975
- ^ Bergh & Löfström 1976
- ^ a b Triebel 1995
- ^ Bessel potential spaces with variable integrability have been independently introduced by Almeida & Samko (A. Almeida and S. Samko, "Characterization of Riesz and Bessel potentials on variable Lebesgue spaces", J. Function Spaces Appl. 4 (2006), no. 2, 113–144) and Gurka, Harjulehto & Nekvinda (P. Gurka, P. Harjulehto and A. Nekvinda: "Bessel potential spaces with variable exponent", Math. Inequal. Appl. 10 (2007), no. 3, 661–676).
- ^ Lunardi 1995
- ^ In the literature, fractional Sobolev-type spaces are also called Aronszajn spaces, Gagliardo spaces or Slobodeckij spaces, after the names of the mathematicians who introduced them in the 1950s: N. Aronszajn ("Boundary values of functions with finite Dirichlet integral", Techn. Report of Univ. of Kansas 14 (1955), 77–94), E. Gagliardo ("Proprietà di alcune classi di funzioni in più variabili", Ricerche Mat. 7 (1958), 102–137), and L. N. Slobodeckij ("Generalized Sobolev spaces and their applications to boundary value problems of partial differential equations", Leningrad. Gos. Ped. Inst. Učep. Zap. 197 (1958), 54–112).
References
- Adams, Robert A. (1975), Sobolev Spaces, Boston, MA: Academic Press, ISBN 978-0-12-044150-1.
- Aubin, Thierry (1982), Nonlinear analysis on manifolds. Monge-Ampère equations, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], 252, Berlin, New York: Springer-Verlag, ISBN 978-0-387-90704-8, MR681859.
- Bergh, J.; Löfström (1976), Interpolation Spaces, An Introduction, Springer-Verlag, ISBN 9787506260114
- Evans, L.C. (1998), Partial Differential Equations, AMS_Chelsea.
- Maz'ya, Vladimir (1985), Sobolev spaces, Springer-Verlag.
- Lunardi, Alessandra (1995), Analytic semigroups and optimal regularity in parabolic problems, Basel: Birkhäuser Verlag.
- Nikodym, Otto (1933), "Sur une classe de fonctions considérée dans l'étude du problème de Dirichlet", Fund. Math. 21: 129–150, http://minidml.mathdoc.fr/cgi-bin/location?id=00113509.
- Nikol'skii, S.M. (2001), "Imbedding theorems", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=i/i050230.
- Nikol'skii, S.M. (2001), "Sobolev space", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=S/s085980.
- Sobolev, S.L. (1963), "On a theorem of functional analysis", Transl. Amer. Math. Soc. 34 (2): 39–68; translation of Mat. Sb. , 4 (1938) pp. 471–497.
- Sobolev, S.L. (1963), Some applications of functional analysis in mathematical physics, Amer. Math. Soc..
- Stein, E (1970), Singular Integrals and Differentiability Properties of Functions,, Princeton Univ. Press, ISBN 0-691-08079-8.
- Triebel, H. (1995), Interpolation Theory, Function Spaces, Differential Operators, Heidelberg: Johann Ambrosius Barth.
- Ziemer, William P. (1989), Weakly differentiable functions, Graduate Texts in Mathematics, 120, Berlin, New York: Springer-Verlag, ISBN 978-0-387-97017-2, MR1014685.
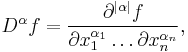
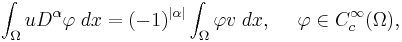
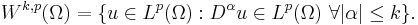
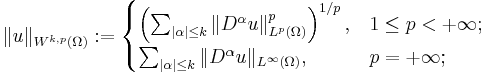
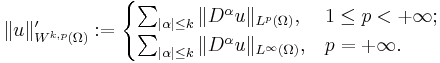
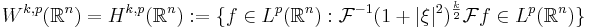
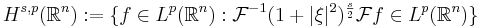

![\big[ W^{k,p}(\mathbb{R}^n), W^{k%2B1,p}(\mathbb{R}^n) \big]_\theta = H^{s,p}(\mathbb{R}^n), \quad 1 \leq p \leq \infty, \theta \in (0,1), s= (1-\theta)k %2B \theta (k%2B1).](/2012-wikipedia_en_all_nopic_01_2012/I/9a9e1b3f345676c891a990632e5b56c9.png)